VC Incentive Alignment
Shared ownership is supposed to align incentives. If two founders each own 50% of a given company, then they will tend to want the same things for that company. But consider a founder who owns 99% of one company and an investor who owns 1% of 99 companies– do these actors always have the same incentives? Not necessarily. To see why, consider the following model.
Suppose that the ultimate value of a company can be modeled by a log normal distribution $X \sim \mathcal{LN}(\mu, \sigma^2)$. Assuming log utility, a single founder who owns the entire company receives the expected utility,
\[U_F = E[\log(X)] = \mu.\]That is to say, the utility scales only with the mean and does not depend on the variance, as the fluctuations in returns are precisely canceled by the log utility function: the founder in this scenario is perfectly indifferent to the variance.
Now consider the case of an investor who owns a $1\%$ stake in $100$ companies, each of whose valuations is independently and identically distributed as $\mathcal{LN}(\mu, \sigma^2)$. The investor’s portfolio $Y = \frac{1}{N}\sum_{i=1}^{100} X_i$ is the arithmetic mean of $N$ log-normal random variates. The portfolio has the first two moments:
\[\begin{align*} E[Y] =& \exp{\left(\mu + \frac{\sigma^2}{2}\right)}\\\\ V[Y] =& \frac{(\exp{(\sigma^2)} - 1)\exp{\left(2\mu + \sigma^2\right)}}{N},\\ \end{align*}\]and gives the investor utility:
\[U_I = \log(Y).\]To estimate the quantity $U_I$, we can appeal to a useful approximation for functions of random variables. For sufficiently well-behaved functions $f$ and random variables $X$ we may Taylor-expand inside the expectation and write:
\[\begin{align*} E[f(X)] =& E[f(E[X]) + f'(E[X]) (X - E[X]) + f''(E[X]) \frac{(X - E[X])^2}{2} + \mathcal{O}(X^3)]\\ \approx& f(\mu) + \frac{f''(\mu)}{2}V[X].\\ \end{align*}.\]Applying this idea to $\log(Y)$, we obtain:
\(E[\log(Y)] \approx \log(E[Y]) + \frac{-V[Y]}{2 E[Y]^2}\).
Plugging in the relevant quantities and simplifying, we arrive at:
\[\begin{align*} E[\log(Y)] \approx& \mu + \frac{\sigma^2}{2} - \frac{\exp{(\sigma^2)} - 1}{2 N}\\ \approx& \mu + \frac{\sigma^2}{2}, \end{align*}\]the last line obtaining asymptotically when N is large. Notice that, whereas the sole founder’s utility was simply $\mu$, the investor’s utility contains an additional term $\frac{\sigma^2}{2}$ that scales with the variance.
What does this portend for incentive alignment between founders and investors? Generally speaking, both parties benefit from making $\mu$ go up. However, investors can benefit from increasing the quantity $\mu + \frac{\sigma^2}{2}$ as well. This is true even if $\mu$ itself goes down, so long as the decrease in $\mu$ is more than offset by an increase in $\sigma^2$, i.e. $\Delta \sigma^2 > -2\Delta \mu$.
This argument is summarized graphically in the diagram below:
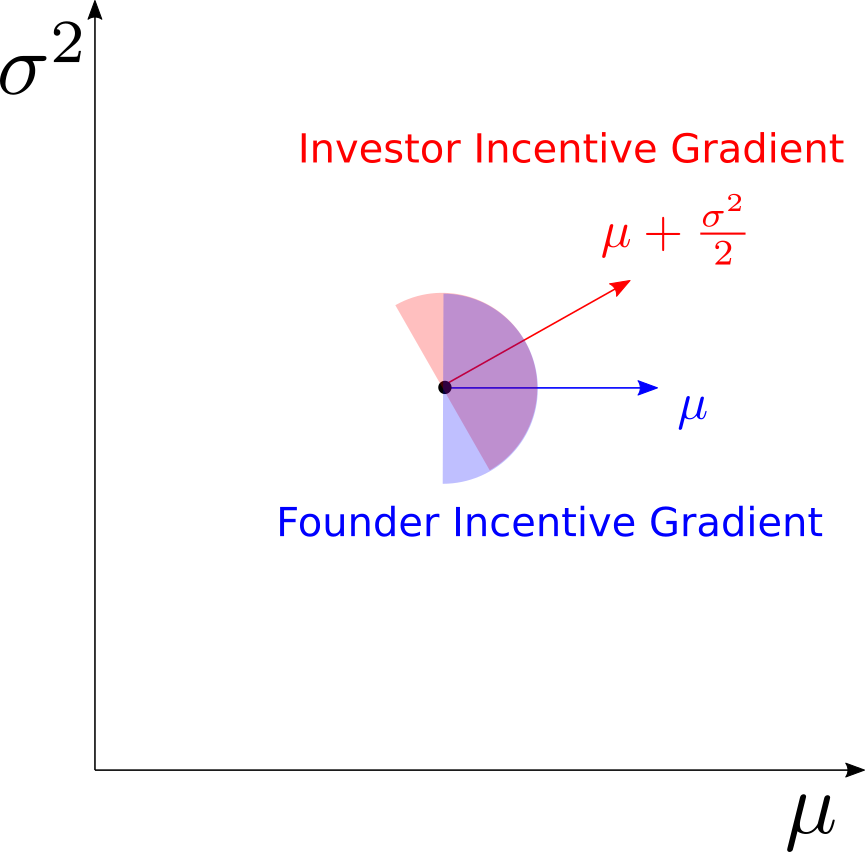
Considering the company as a point in a parameter space, the founder benefits most from pushing the state of the business in the direction of the blue arrow. An infinitely diluted investor, however, benefits most from pushing things in the direction of the red arrow. The shaded hemispheres show the directions that would be acceptable to either party. The purple sector denotes the area of mutual benefit. The opposing red and blue sectors indicate the axis of antagonism: directions that would be preferred by one party but not the other.
Are founders and investors explicitly thinking of companies as log-normal random variables? Not necessarily. This is, of course, a highly stylized model that caricatures one particular dynamic. But every day, founders get up and tweak parameters that make successes of various sizes more or less likely. It’s not such a leap to think of startups as random variables whose parameters you can modify with effort.
A friend of mine with a lot of experience in the startup world noticed that investors would come in and make suggestions that didn’t seem to reflect the best interests of the company. These suggestions were mostly of the swing-for-the-fences variety, encouraging the founders to take the company in directions that had a small chance of spectacular success, even if the modal outcome was failure. To the founders, who presumably didn’t relish the thought of betting years of hard work on a lottery ticket, this advice seemed very bad. Did the investors simply not know what they were talking about?
More likely, the investors did know what they were talking about– they were just giving the advice that suited their own interests, which might not necessarily be yours.
